Fraction Strips Up To 12

I recently noticed that the fraction circles and fraction strips on the website showed some inconsistencies and needed comeback. If you aren't familiar with these manipulatives, they are mostly used for learning nigh fractions and oftentimes for comparing fractions. With some creativity, they can be used for a wide diversity of activities, some of which I'll suggest later on. Fraction strips are wide rectangles (strips) that are all the same length, but they are divided into different partial sections. Each strip is worth ane whole, just they are divided into the same number of sections every bit the denominator of the fraction. For example, the thirds strip is divided into three segments and the tenths strip is divided into ten segments. Fraction circles are much the same except they are circular and the fractions are pie-shaped sections (circle sectors). To view all of the fraction strips and fraction circles visually, visit the search page on Math-Drills.

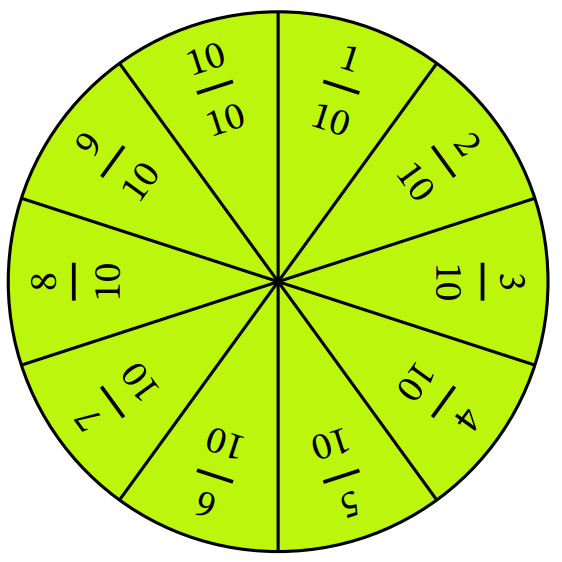
The tenths strip and the tenths circumvolve are shown for comparing.

Colors

Ane of the major changes in both the fraction strips and fraction circles was the coloring. Previously, there were black and white and color versions, just I thought the black and white version lacked dissimilarity to the groundwork of the page, so I also made a gray version. Of grade, the black and white versions are still quite valuable as you or your students can color them for your ain purposes and activities (come across further downwardly). The color versions use a color scheme that was developed by Sasha Trubetskoy which was a God-send because creating a color scheme is a really difficult thing to do! 20 different colors that when compared to each other are different enough to be distinguishable is no easy task. Educators should always keep in mind, however, that a significant portion of the population is color-bullheaded to some degree, so intendance must exist taken when asking anyone to distinguish colors.

Smart Fraction Strips

The "classic" fraction strips on the website are presented in numerical order of their denominators, but I thought it would exist interesting to also have a version with a "smart" order: 1 that showed similar strips adjacent to one another. The order of the denominators on the "smart" fraction strips is: ii, 4, 8, 12, 16, 20, 15, 10, 5, three, 6, ix. The idea was to accept a group that included 2, four, eight, 12, 16, 20; a 2nd group that included xx, 15, 10, 5; and a 3rd group that included 3, 6, 9. Sevenths and elevenths aren't included on the smart fraction strips every bit they don't play well with the other strips, so it wouldn't be smart to include them. Of grade, if they are cut out, you can put them in all sorts of different orders!

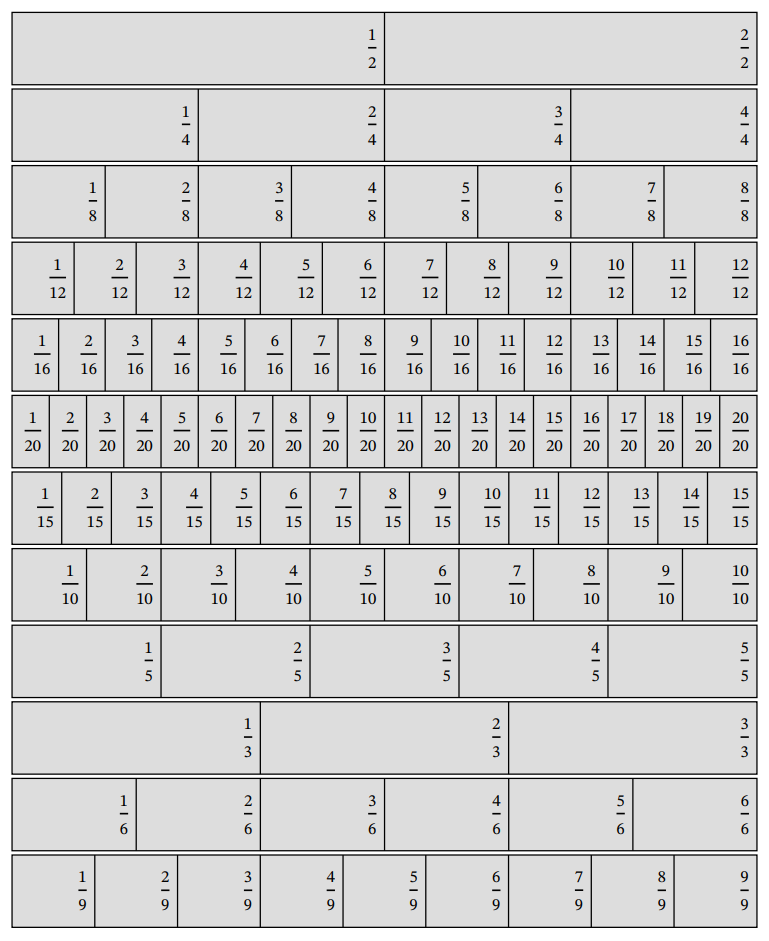
Yous may besides notice that there is no strip for one whole. After much idea and consideration, I excluded it as every strip is worth one whole and I could use the actress infinite to include another fraction strip. In the case of the archetype fraction strips, twentieths were included as they have more fractions in mutual with the other strips than say, sixteenths. The smart fraction strips include fifteenths, sixteenths and twentieths.

Labels

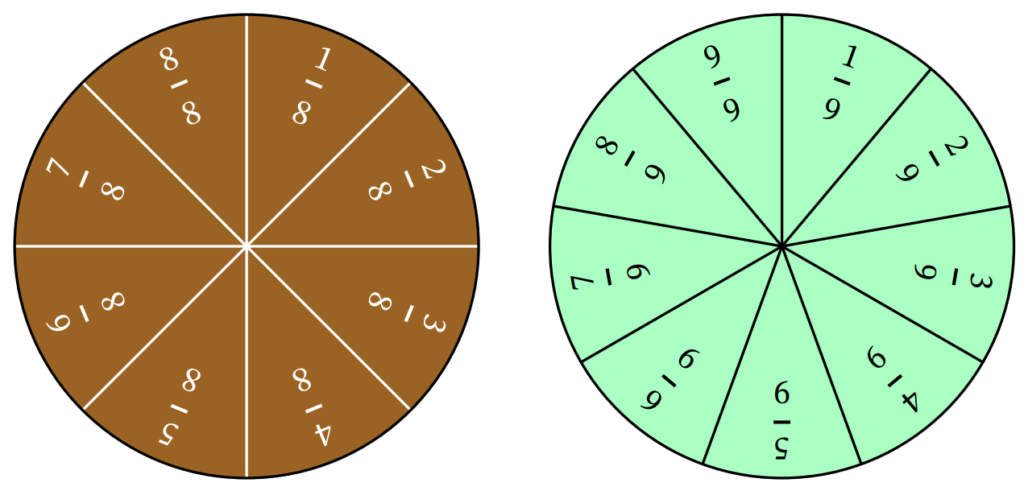
The sometime strips and circles had labeled and unlabeled versions and then practise the new ones. I had a scrap of a struggle with the circles deciding whether I should rotate the text around the circle (I did) and whether the numerators should be incremented (also did). Those 2 items were not implemented on the old versions, so hopefully they piece of work for you. Using some more color theory, I also had to decide whether the labels and dividing line segments should be in black or white for each strip and circle. At that place are formulae and guidelines out there that give unlike weights to the RGB values of a colour and allow you decide mathematically whether a certain background color would look improve with black or white text. I think the best indication of whether this was washed well or not is to look at a thumbnail version of the worksheet to see if the numbers tin can still be read and I'chiliad quite confident that this is the case. I also printed diverse versions to make sure they looked proficient on newspaper. In the fraction circles below, note that one has text and dividers in white and the other in blackness based on the groundwork color.

Activities

Exploring fractions with strips can be done to discover equivalent fractions without cutting anything out, only a straight edge like a ruler is handy. The smart fraction strips facilitate this exploration as similar fractions are nearly to one another. Students simply expect for partial amounts that "line-up" and can see how these fractions must exist worth the aforementioned as they take up exactly the same amount of each strip. For example, 1/two, 2/4, 3/6, iv/8, v/ten, half-dozen/12 and ten/20 all line up on the fraction strip pages.

Overhead transparencies can be your all-time friend when it comes to comparing fraction strips or fraction circles. The thought is to have one copy on an overhead transparency and ane re-create on a piece of paper. Cutting out strips or circles from the transparency version is optional, simply makes information technology easier to compare. Students simply position the transparency version over the paper version and compare various fractions. For example, if they were comparison sixths and ninths, they would position the sixths transparency over the ninths on the paper, line upward the nada line (left most line on fraction strips and top vertical line that points n on the fraction circles) and see what matches. two/6 = 3/9 and 4/six = 6/9, in this case. How many equivalent fractions tin can they detect on their own? Can they use these manipulatives to help them consummate a comparing fractions worksheet? Not-permanent markers can also be used on the transparency or the black and white version to model different fractions.

Adding fractions generally involves cutting fraction strips and circles into individual sections, so they can exist "fit together," only overlapping is also a possibility. For example to add ii/five and iii/10 and using the overhead transparency version cut up, students would line upward the get-go ii fifths sections left to right so place the first three tenths sections to the correct of the fifths. A little tape will facilitate moving them around on a paper copy to see what two fifths and three tenths matches and they should find matches of seven/10 and 14/20.

Subtracting fractions is done in a similar way to calculation fractions, but instead of arranging them all in 1 row (fraction strips), the original corporeality (the minuend) is arranged in the showtime row and the amount to exist subtracted (the subtrahend) is placed in a 2d row, and then that it aligns with the finish of the first row. The gap at the get-go of the second row is the difference and gets compared to a paper copy. With fraction circles, the subtrahend overlaps the minuend and the sector that isn't overlapped is the deviation. Using 2/5 – 3/10, students would notice that the difference would line upwardly with 1/10 or 2/20.

Many other activities are possible such as determining combinations of two, iii or four fractions (or more) with different denominators add up to one whole (or any other fraction); using folding to make fraction strips or circles (hint: halves, quarters and eighths are easy); using fraction circles to brand pie charts; multiplying and dividing fractions; using fraction circles intact to make equal probability spinners or cut up to make weighted probability spinners; bending measurement to explore circle backdrop; creating games; using strips and circles for fractions greater than one; etc.